こんにちは、Excelスタティスティックスストラテジーヴァイスアクティヴィストの鈴木です。本日は万能ツールであるMicrosoft Excelを用いて有名なパラドックスをシミュレーションし、直感にそぐわない結論が現実に合致することを確認していきましょう。
今回扱うパラドックスは、モンティホール問題と言われるもの。その問いを、Wikipediaから引用します。
プレイヤー(回答者)の前に閉じられた3つのドアが用意され、そのうちの1つの後ろには景品が置かれ、2つの後ろには、外れを意味するヤギがいる。プレイヤーは景品のドアを当てると景品をもらえる。
最初に、プレイヤーは1つのドアを選択するがドアは開けない。次に、当たり外れを事前に知っているモンティ (司会者)が残りのドアのうち1つの外れのドアをプレイヤーに教える(ドアを開け、外れを見せる)。ここでプレイヤーは、ドアの選択を、残っている開けら れていないドアに変更しても良いとモンティから告げられる。
プレイヤーはドアの選択を変更すべきだろうか?
一見、はずれドアの情報を知ったところで、何も変わらない。残ったドアの向こう側が、その情報を知る前後で変わるわけでもないので、そこで乗り換えてあたりを引く確率が高まるとは思えません。
Excelで試してみる
では、具体的な値を使って確認してみましょう。Excelの登場です!
1回の試行について、こんなスプレッドシートを作りました。なお、選択を変えない人をAさん、乗り換える人をBさんとしています。
1回の試行について、こんなスプレッドシートを作りました。なお、選択を変えない人をAさん、乗り換える人をBさんとしています。
説明していきましょう。
「あたりドア」と「A予想」は、RAND関数で毎回再計算します。「A判定」では、あたりドアとA予想が一致していれば1、不一致なら0となります。IF関数です!
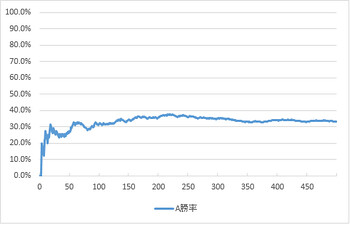
勝率は、その行までの累積あたり回数を、試行回数で割っています。ここではAさんは最初に4回もはずれ、10回中2回しか当たっていません。この時点で、勝率は20.0%。これを500回繰り返した時のグラフが以下です。
「あたりドア」と「A予想」は、RAND関数で毎回再計算します。「A判定」では、あたりドアとA予想が一致していれば1、不一致なら0となります。IF関数です!
勝率は、その行までの累積あたり回数を、試行回数で割っています。ここではAさんは最初に4回もはずれ、10回中2回しか当たっていません。この時点で、勝率は20.0%。これを500回繰り返した時のグラフが以下です。
試行が少ない時には勝率がぶれますが、試行を重ねると、33.3%あたりに収束していくことがわかります。RANDを使っているので、再計算のたびにグラフが変わりますが、傾向は同じ。3回に1回あたるというのは直観になじみますよね。
次に「司会者」。
上で述べた通り司会者は、Bくんが選択していない2つのドアから1つを選んで開くことになります。ここではRAND、MAX、MIN、VALUE、MATCHといった各種関数を駆使した気持ちの悪いExcel数式で、司会者が開くドアを決定しています。もっとさわやかに書けると思ったのですが、非常に汚い数式なのでお見せできません。Excel関数設計のためのデシジョンテーブルまで書いてしまいました。素晴らしいですね。
上で述べた通り司会者は、Bくんが選択していない2つのドアから1つを選んで開くことになります。ここではRAND、MAX、MIN、VALUE、MATCHといった各種関数を駆使した気持ちの悪いExcel数式で、司会者が開くドアを決定しています。もっとさわやかに書けると思ったのですが、非常に汚い数式なのでお見せできません。Excel関数設計のためのデシジョンテーブルまで書いてしまいました。素晴らしいですね。
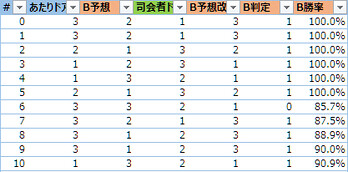
「B予想改」は、選ぶドアを変えるBくんがあらためて選んだドアです。実質的には、3つのドアのうち1枚は開かれ、もう1枚はもともと選んでいるのですから、選択の余地はありません。「B判定」「B勝率」は、Aと同様です。
たとえば#5を見ると、あたりが2で当初予想は1、司会者が3を開いたのでBくんは2を開き、あたりとなっています。一方#6では、あたりも当初予想も3で、司会者は2を開き、Bくんは1を開いてはずれになっています。
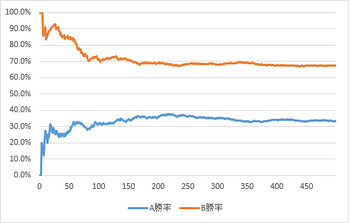
これをグラフにしてみましょう。
おお、66.6%に収束しています!
つまり、ドアを変える戦略の方が、ドアを変えない戦略の2倍、あたりの確率が高いということです。
当初この結果を発表した女性の数学者は、数学会の大御所から「ありえない、数学者失格」くらいの罵倒を受けたそうです。それほど、パラドックスというのは不可思議なもの、そしてExcelは素晴らしいツールということがよくわかりますね。
算数的には意外に素直
ざっくりと理屈も考えておきましょう。
ベイズ確率などちゃんと理解していないので、嘘を書いているかもしれないです。ご指摘ある場合は、平易な言葉でお願いします・・・。
最初からあたりを引いていた場合。乗り換えなければそのままあたり、乗り換えればはずれです。当たり前ですね。
最初にはずれを引いていた場合。乗り換えなければそのままはずれ。乗り換える場合、司会者が開くことができるのは、「最初に選んだドア(はずれ)ではなく、かつ、はずれのもの」なので、選択の余地がありません。そして乗り換える先は、あたりしか残っていません。つまり、乗り換えれば必ずあたります。
最初にはずれを引いていた場合。乗り換えなければそのままはずれ。乗り換える場合、司会者が開くことができるのは、「最初に選んだドア(はずれ)ではなく、かつ、はずれのもの」なので、選択の余地がありません。そして乗り換える先は、あたりしか残っていません。つまり、乗り換えれば必ずあたります。
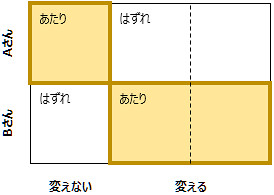
「最初からあたりを引く」確率と、「最初にはずれを引く」確率は、1:2。なので、「最初にはずれて乗り換える」と、「最初にあたって乗り換えない」では、2倍の差があるんですね。絵にすると、こういうことになります。
こうしてみると、乗り換える方が有利に決まっていますね。パラドックスって不思議ですね、そしてExcelは素晴らしい。ということで、これ系の話で特によかった本のAmazonリンクと、以前書いた記事をおいておきますね!


リスク・リテラシーが身につく統計的思考法―初歩からベイズ推定まで (ハヤカワ文庫 NF 363 〈数理を愉しむ〉シリーズ) (ハヤカワ文庫NF―数理を愉しむシリーズ)
- 作者: ゲルト・ギーゲレンツァー,吉田利子
- 出版社/メーカー: 早川書房
- 発売日: 2010/02/10
- メディア: 文庫
- 購入: 19人 クリック: 189回
- この商品を含むブログ (28件) を見る