ヤマハの小池さん主催の「（ソフトウェア品質技術者のための）R勉強会」の第2回が行われましたので、復習をかねてエントリを書きます。なお、当日のつぶやきまとめはコチラにあります。
今回のテーマは、『例題で学ぶ統計的方法』の第7話「散布図と相関係数」、第8話「回帰曲線」。「ソフトウェア品質技術者」がもっとも使う道具がこの2つと言えるかも知れません。ともに、基本は知ったつもりでいながら、学んだところが大きかったです。
![例題で学ぶ統計的方法 [改訂版]](https://images-fe.ssl-images-amazon.com/images/I/41H2DBaqRCL._SL160_.jpg "例題で学ぶ統計的方法 [改訂版]")
散布図を書いてみる
まずは全データで。
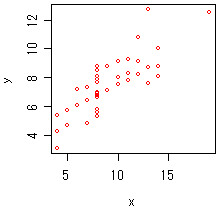
何はともあれ、演習で使ったデータセット（Anscombe のデータ）をで、散布図を書いてみましょう。データセットの44点をプロットしたのが、下のグラフ。
「ぼんやり、右肩あがり」程度しか、傾向は見いだせませんね。
層別で。
実は上のグラフは4種類のデータをいっしょくたにしたものなので、描き分けてみます。グラフ描画のダイアログで「層別」を選択し、平滑線も入れて出力した結果が、以下。
分けると、傾向が見えました。赤○と青+は、右肩上がり。緑△は2次曲線。水色×は、Y軸に垂直な傾向がありますね。
データのサブセットを作る。
では、この青+のみのプロットをしてみましょう。データを絞ってグラフを描く方法は（少なくとも）2つあります。
|
絞ったデータ自体を何度も使いたいなら、①がいいでしょうね。手順は、メニューの [データ] - [アクティブデータセット] - [アクティブデータセットの部分集合の抽出] から。
ダイアログは、入力した値を覚えておいてくれないので、一度実行したら、コマンドを直接叩く方が早いでしょう。下のコマンドは、初めに使っていたデータセット Ans01 から、変数 layer の値が 「c」であるものを選び、さらに変数 layer 自体は省いたデータセット Ans02 を定義しています。
ダイアログは、入力した値を覚えておいてくれないので、一度実行したら、コマンドを直接叩く方が早いでしょう。下のコマンドは、初めに使っていたデータセット Ans01 から、変数 layer の値が 「c」であるものを選び、さらに変数 layer 自体は省いたデータセット Ans02 を定義しています。
| > Ans02 <- subset(Ans01, subset=layer=="c", select=c(x,y)) |
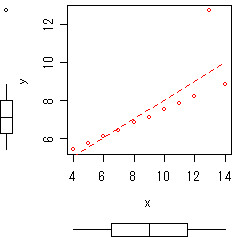
この Ans02 で散布図、および最小二乗直線を描くと、
不自然なほどきれいな直線に乗っている。が、どうも右上の点は、傾向から外れているように見える・・・。
外れ値を除去してみる
さて、全体の傾向から外れているからといって、それが「間違っている」「意味がない」ということにはなりませんが、全体の傾向をより精度よく調べるために、これを外したい。
ただ、「外す」には何らかの指標がほしいものです。恣意的に外すべきではない。ではどんな方法があるでしょうか。
ただ、「外す」には何らかの指標がほしいものです。恣意的に外すべきではない。ではどんな方法があるでしょうか。
簡単なのは、トリム平均というものです。最大と最小の付近の値を取り除いてから平均値をとる。Excel だと TRIMMEAN という関数があって、上下何パーセントを除くかを指定することができます。
四分位（クオンタイル）点からの判定
野中先生に教えていただいた1つの目安は、「箱ひげ図を見て、四分位範囲の1.5倍を超えたらはずれ値の候補とする」というものです。
上の図のように、箱ひげ図は散布図のオプションとして出力できるので、まずはざっくりとはつかめますね。y軸でいうと、箱の上辺が第3四分位、下辺が第1四分位でその幅が四分位範囲です。この幅の1.5倍以上、上辺より上にある、または下辺より下にある場合、はずれ値とみなせるかも、と*1。
四分位範囲の正確な値は、メニューから、[統計量] - [要約] - [アクティブデータセット]。これで数値データセットの基本統計量を出力するコマンドです。
| > summary(Ans02) x y Min. : 4.0 Min. : 5.40 1st Qu.: 6.5 1st Qu.: 6.25 Median : 9.0 Median : 7.10 Mean : 9.0 Mean : 7.50 3rd Qu.:11.5 3rd Qu.: 8.00 Max. :14.0 Max. :12.70 |
なお、四分位点を求めるには、以下。
| > quantile(Ans02[,"y"]) 0% 25% 50% 75% 100% 5.39 6.25 7.11 7.98 12.74 > quantile(Ans02[,"y"],0.75) 75% 7.98 |
今回、y の上の方の外れ値を外すことを考えるので、データセット Ans02 に対する四分位範囲（InterQuartile Range）を求めてみましょう。この表現にたどり着くまでに、試行錯誤で2時間以上かかりました。本当に疲れた。
| > IQR(Ans02[,"y"]) [1] 1.75 |
「第3四分位点から見て、四分位範囲の1.5倍より大きい値」は、
| > quantile(Ans02[,"y"],0.75) + IQR(Ans02[,"y"])*1.5 75% 10.625 |
この表現を使って、散布図と最小二乗直線を描いてみます。
この式を、グラフ作成時のデータ絞り込み条件に使ってもいいし、別の変数に代入して、その変数を絞込み条件に使うこともできます。下のコマンドでは、直接絞り込んでいます。
この式を、グラフ作成時のデータ絞り込み条件に使ってもいいし、別の変数に代入して、その変数を絞込み条件に使うこともできます。下のコマンドでは、直接絞り込んでいます。
| > scatterplot(y~x, reg.line=lm, smooth=FALSE, labels=FALSE, boxplots='xy', span =0.5, data=Ans02, subset=y<quantile(Ans02[,"y"],0.75) + IQR(Ans02[,"y"])*1.5) |
外れ値を除いた曲線を描くことができました。確かに、「直線に乗ってるっぽい」ですね。
箱ひげ図の特徴
ところで、はずれ値を除去しても、y軸の箱ひげ図の幅があまり変わっていないことは、大事なポイントです。この「データを多少抜いても、あまり変わらない」箱ひげ図の性質を、ロバスト性というと習いました。
何故、ロバストか。箱ひげ図はデータの順番を見ているので、データが多ければ、はずれ値を外したところで全体への影響は少ない。一方平均なんかは、値そのものが計算に効いてくるので、外れ値の影響を思い切り受けるわけです。なるほど・・・。
何故、ロバストか。箱ひげ図はデータの順番を見ているので、データが多ければ、はずれ値を外したところで全体への影響は少ない。一方平均なんかは、値そのものが計算に効いてくるので、外れ値の影響を思い切り受けるわけです。なるほど・・・。
極端なデータセット(96, 1, 1, 1, 1) を考えてみましょう。
平均値は20、中央値は1。
一方、はずれ値「96」を外すと、平均値は1に大きく変化しますが、中央値は依然として1（=(1+1)/2）なのです。
外れ値の目安を聞いたときに、「外れ値を外すと1.5倍の範囲も変わって、やってもやっても新しいはずれ値が出るのでは？」と思ったのですが、この性質によって、この「タマネギの皮むき」をある程度回避できるのですね。
平均値は20、中央値は1。
一方、はずれ値「96」を外すと、平均値は1に大きく変化しますが、中央値は依然として1（=(1+1)/2）なのです。
外れ値の目安を聞いたときに、「外れ値を外すと1.5倍の範囲も変わって、やってもやっても新しいはずれ値が出るのでは？」と思ったのですが、この性質によって、この「タマネギの皮むき」をある程度回避できるのですね。
その2では、求めた最小二乗曲線が「どのくらい妥当なのか」という話と、最小二乗曲線の注意点について、学んだことを書きます。
関連リンク
*1:2011/11/22: 「この幅1.5個分よりメディアンから離れていたら」としていた記述を修正しました。また、以降の「四分位偏差」も「四分位範囲」に修正しました。野中先生ありがとうございます。
