勉強会からずいぶん間が空きました。週明けには第4回です!
原因結果グラフ(CEG)の5つの制約について考えてみました。
テストケースを減らす3つのプロセス
CEGTestを動かしてみただけでの判断となりますが、CEGからデシジョンテーブルが作られるまでに、テストケースを減らすプロセスが大きく3つあるようです。
- 真偽パターンの優先度付け
- 原子的な論理式の詰め込み
- 制約の付与
(1)と(2)は、その1で考察しました。
(1)は、A∧Bについて、A・Bともに偽になるような真偽パターンをカバレッジ表から落としています。∨についても同様。
(2)は、適切に分解された個々の論理式の真偽パターンをうまく組み合わせることで、全体として少数のパターンに集約しています。
(2)は、適切に分解された個々の論理式の真偽パターンをうまく組み合わせることで、全体として少数のパターンに集約しています。
(3)の制約で減らすのは、「普通の使い方をしていれば起こらない真偽パターン」です。
たとえばWebサイトで、「チェックボックス1がonのときだけ、テキストボックス1がenableになる」という制約を設けたところで、送信時のデータの書き換えは容易ですから、チェックボックス1がoffなのにテキストボックス1にも入力があるようなデータを送りつけることはできます。ですから、そのようなパターンのテストを「しなくてもよい」ということにはならず、何らかの形では確認する必要はある。で、そのような確認は行ったことを前提に、CEGやデシジョンテーブルでは「普通は」出てこないはずの組み合わせを省く、ということになります。
たとえばWebサイトで、「チェックボックス1がonのときだけ、テキストボックス1がenableになる」という制約を設けたところで、送信時のデータの書き換えは容易ですから、チェックボックス1がoffなのにテキストボックス1にも入力があるようなデータを送りつけることはできます。ですから、そのようなパターンのテストを「しなくてもよい」ということにはならず、何らかの形では確認する必要はある。で、そのような確認は行ったことを前提に、CEGやデシジョンテーブルでは「普通は」出てこないはずの組み合わせを省く、ということになります。
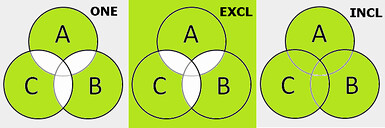
「集合系」制約:ONEとINCLとEXCL
この3つは直感的にわかりやすいですね。複数の選択肢がある場合、ONEは「必ず1つだけが真となる」、EXCLは「真になるのはせいぜい1つだけ」、INCLは「少なくとも1つ以上が真になる」という制約です。お約束のベン図。
白い部分に相当する真偽パターンは、テストケースから除外されます。たとえばONE制約はラジオボタンのイメージ。2つ以上を選択したり、1つも選択しないようなテストケースはない、ということです。
ちなみに、上述した(1)~(3)によるケース削減は排他的ではないので、制約を設けてもケースが減らないことがあります。
たとえば Effect ⇔ A∧B∧C という論理式では、(1)により、A・B・Cの任意の2つ以上が偽になるケースは現れません。よって、この3つにINCL制約を付与しても、INCL制約により削減される「A・B・Cすべてが偽」のケースは元々現れていないので、カバレッジ表は変わらないということです。
たとえば Effect ⇔ A∧B∧C という論理式では、(1)により、A・B・Cの任意の2つ以上が偽になるケースは現れません。よって、この3つにINCL制約を付与しても、INCL制約により削減される「A・B・Cすべてが偽」のケースは元々現れていないので、カバレッジ表は変わらないということです。
「順序系」制約その1:REQ
難しいのが順序系です。『ドリル』によるとREQは、
Require(前提)の略で、あるノードが真になるために、事前に真になっていることが必要となるノードを指定
とあります。これは論理学でいうと、A⇒B(AならばB)という論理に当たります。「AならばB」なので、真理値としては、A真・B真なら真、A真・B偽なら偽。
これはわかりやすいのですが、A偽B真なら真。A偽B偽でも真。つまり、「Aが偽なら、Bが真だろうと偽だろうと、A⇒Bは真」という、ちょっとわかりづらい定義になっています。「おれ、この戦いが終わったら結婚するんだ」という命題で言うと、「戦いが終わらなかった場合は、結婚しようとしまいと嘘にはならない」ということで真なんだ。と考えることにしましょう(ただし死亡フラグは真になる)。
ちなみに、A⇒Bは、¬A∨B と同値(A真B偽の時だけが真理値が偽になる)です。
これはわかりやすいのですが、A偽B真なら真。A偽B偽でも真。つまり、「Aが偽なら、Bが真だろうと偽だろうと、A⇒Bは真」という、ちょっとわかりづらい定義になっています。「おれ、この戦いが終わったら結婚するんだ」という命題で言うと、「戦いが終わらなかった場合は、結婚しようとしまいと嘘にはならない」ということで真なんだ。と考えることにしましょう(ただし死亡フラグは真になる)。
ちなみに、A⇒Bは、¬A∨B と同値(A真B偽の時だけが真理値が偽になる)です。
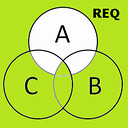
では、ここで除外される真偽パターンは何なのでしょう。
上のベン図は、ややこしいのですが、(A→B)∧(A→C) を表しています。白い部分は、「BかCの少なくとも一方が偽なのに、Aが真になっちゃっている」という部分です。逆にいうと、BとCがともに真になる部分と、Aが真になっていない部分は対象です。
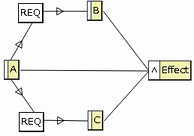
さて、CEGTestでREQ制約を書いてみましょう。
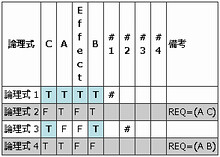
AからREQを経由してBへ、矢印が伸びています。これは、AがBに先立つという意味ではありません。「Aが真になるためには、Bがあらかじめ真でなくてはならない」という意味です。よってカバレッジ表でも、Aが真なのにBが偽であるようなケースが灰色になっています。
BがAに先立つのだから、矢印もBからAに向かいそうなものですが、実際は逆。初めは違和感がありましたが、論理式が「A⇒B」であることを考えると、CEG上の矢印も、同じ方向の方が自然ですね。この「A⇒B」と、カバレッジ表に現れる「REQ=(A B)」も、同じものです。
「順序系」制約その2:MASK・・・?
さあ、このままMASKについての理解をメモしていきたいところですが、、、MASKは難しすぎる。MASKを理解するための非常に単純な例題を考えてみましたが、それすら解けないというアリサマ。
次回はその苦悩を、勝手に共有させていただこうと思います。
次回はその苦悩を、勝手に共有させていただこうと思います。