未だに勉強会の復習が終わっていないわたしです。
原因結果グラフ(CEG)が難しいなあと思う理由の1つに、解答が一意でないという点があります。CEGに限ったことではないかも知れませんが、「真実はいつもひとつ!」(by 江戸川)だといいのに。
今夜は、『ソフトウェアテスト技法ドリル』に掲載された、Myersの三角形についてのCEGを、Nifty加瀬正樹さん作のCEGTestで恐る恐る書き換えてみました。

- 作者: 秋山浩一
- 出版社/メーカー: 日科技連出版社
- 発売日: 2010/10/01
- メディア: 単行本
- 購入: 7人 クリック: 153回
- この商品を含むブログ (19件) を見る
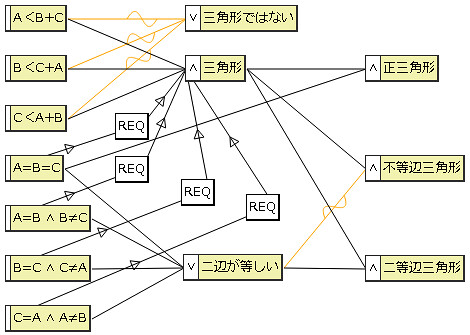
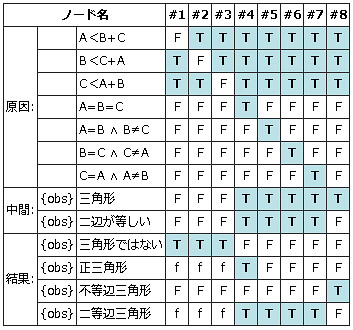
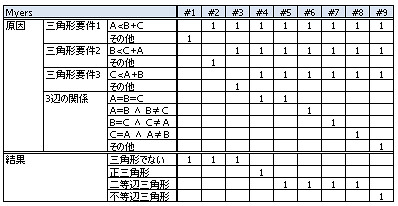
まず、『ドリル』に載っているCEGと、デシジョンテーブルは以下です*1。
原因ノードの下の4つ、3辺の関係を判定する前に、そもそも「三角形である」ことを要求しています。でも、REQ制約が4つもあると、グラフが入り組みまくってしまい、どうも見晴らしが悪い。しかしこのREQを外してしまうと、A<B+Cが満たされていない、つまり三角形ではない条件に対して、A=B=Cが真になるケースを組み合わせてしまったりするので、困ります。
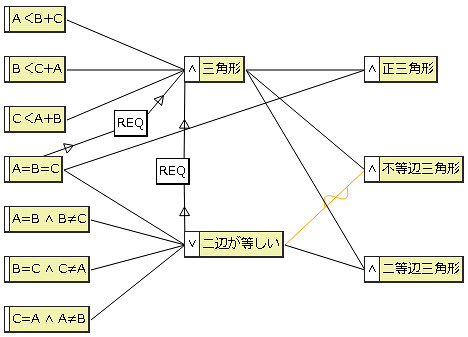
なので、せめて「A=B=C」と「二辺が等しい」の2つのノードから、REQ制約をかけることにしました。「A=B=C」には、間接的に2回REQ制約がかかっている気もしますが・・・。いいのかな。デシジョンテーブルは変化ありません。
またここでは、「三角形ではない」という結果ノードも削除しています。「正三角形」「二等辺三角形」「不等辺三角形」のすべてが偽なら、自動的に「三角形ではない」ため。原因ノードには、「A≠B ∧ B≠C ∧ C≠A」がなく、他の4つの条件の補集合になっていることから、結果ノードについてもそうしたいなーというところです。あと、ノードはできるだけ減らしたい。
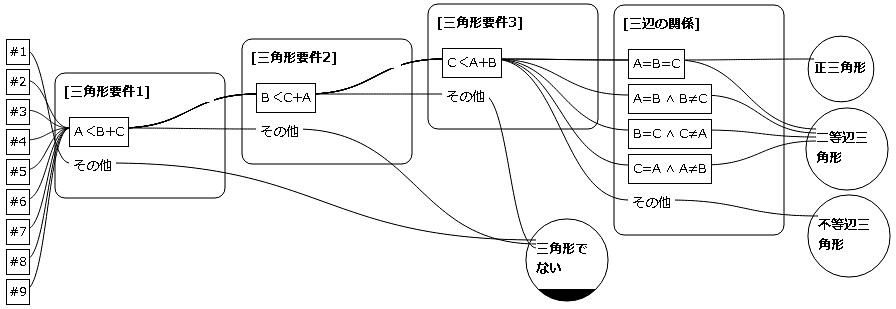
では次に、Meyersの三角形についての原因流れ図(CFD)を、これまた加瀬さん作のDrawCFD(プロトタイプ)で描いてみます。
こちらは、「三角形ではない」という補集合を明示する必要がありますね。
でかっ!でも何か優雅だぜ、flow。
流れは9本あり、CEGに比べて1つ多いようですが、A=B=Cの場合は正三角形でもあり二等辺三角形でもあるという論理関係が、CEGでは1つ、CFDでは2つのケースになっていることによります。
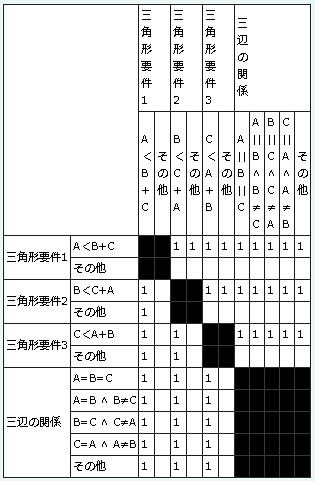
デシジョンテーブルはこんな感じ。
2011年5月12日時点では、デシジョンテーブルの窓に「総当りチェック」というボタンがあり、2因子に対する総当り表のようなものが表示されます。セルが埋まっていない部分は、組み合わせのケースがない、というチェックをするものなのかな・・・?*2
とりあえず、CEGとCFDの練習をして、デシジョンテーブルの一致を確認したところで、今夜のお勉強終わり*3。
*1:ちなみに、ノード名に半角の小なり「<」を使うと、デシジョンテーブルではそのノード名が正しく表示されないようです。
*2:加瀬さんのブログ(のコメント欄)にて、秋山浩一さんとの会話で言及がありました。「2機能間の組み合わせ漏れを検出」か・・・。CFDの言葉でいうと、同値クラス同士を組み合わせているかということでしょうかね。埋まらないセルも、ありそうだ。(2011/5/12) softest.cocolog-nifty.com また、以下のように加瀬さんからコメントいただきました。
総当たりチェック表は、流れ図をもれなく抽出しているかを確認するための表です。 単体テストでは有効系の組み合わせは全て網羅したほうがいいので、空欄の中で有効系×有効系のものがあれば、流れ図を追加する、という使い方になります。
*3:これもコメント欄にあった、流れパターンの網羅性の確認のアイデアから、以下2点についても確認。①一度も「1」にならない原因がないこと。②一度も「1」にならない結果がないこと。(2011/5/12)